題名にも記載のとおり、かのアインシュタインは、「複利は人類最大の発明」と言ったそうです。
確かに、投資をしている人にとって、複利の効果を享受している人も多いでしょう。
複利の効果は、ベースとなる金額や、追加投資も重要な要素ですが、それ以上に
時間を味方につける
という視点が最も重要です。
今回は、具体的な数値を用いて、誰にでも実践可能で、一日でも早く手掛けたい複利効果について、紹介します。
【人類最大の発明】アインシュタインも認めた複利の効果を改めて確認
今回紹介する内容は、以下の通りです。
・複利のロジックは?
・100万円を運用した場合の検証
まず、基本的なところとして、複利のロジックとはどのようになっているのか、確認してみます。
そして、実際にその複利のロジックを使うと、100万円がどのように推移していくのか、
100万円を50年間寝かせたままにする場合と、
最初の元本100万円から、毎年100万円ずつ入金して運用していく場合、
それぞれについて確認してみます。
S&P500に見るこれまでの実績は?
まずはじめに、アメリカの代表的な株価指数である、S&P500について、確認してきます。
S&P500とは?
アメリカを代表する大型株である500社の銘柄で構成されている指数です。
具体的な銘柄としては、一例として
・ヘルスケア株指数:ジョンソン・エンド・ジョンソン、ファイザー、ユナイテッド・ヘルスなど
・金融株指数:バークシャー・ハサウェイ、JPモルガン・チェース、バンク・オブ・アメリカなど
・一般消費財指数:Amazon.com、ザ・ホーム・デポ、マクドナルドなど
・コミュニケーションサービス指数:Alphabet、メタ・プラットフォームズ、ベライゾン・コミュニケーションズなど
といった、普段日本で生活している我々も良く知っている企業が多数含まれています。
銘柄には、時価総額158億米ドル以上、日本円(1ドル155円換算)にして2.4兆円以上のものが入ってくることとなります。
ただし、四半期ごとに銘柄入れ替えが検討されるものの、必ず入れ替えられるという訳ではありません。
1957年からのS&P500の実績は?
S&P500の指数として、1957年以降のデータが残されています。
昨年2023年までの66年間の間における毎年の終値をグラフ化したものを抽出しました。
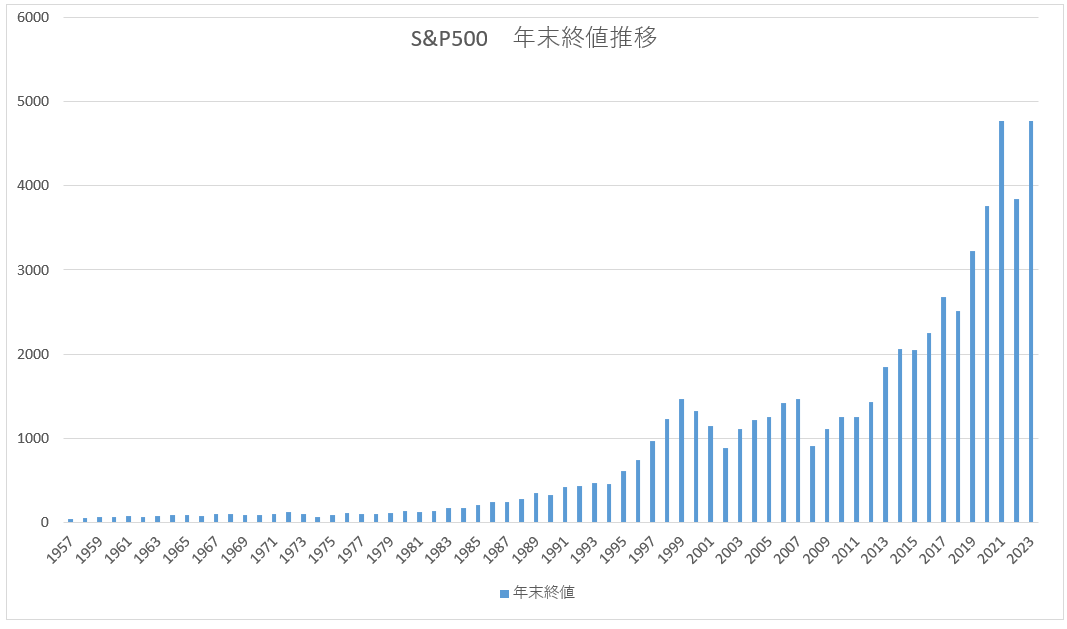
※筆者独自算出
2008年のリーマンショック以降、一貫して伸びてきているのが感覚的にもわかります。
どのタイミングで投資をするかにもよりますが、過去一時的なピークであった1999年や2007年に投資していても、将来はそれをかなり上回る水準となっています。
今後2021年や2023年の水準をどこまで上回るかというのもありますが、2024年11月15日時点で5,870.62であるため、すでに2024年は大きく成長しているといえます。
具体的な数値で確認すると?
つぎに、これらの数値を具体的に一覧で紹介します。
加えて、前年の成長率も付けてみました。
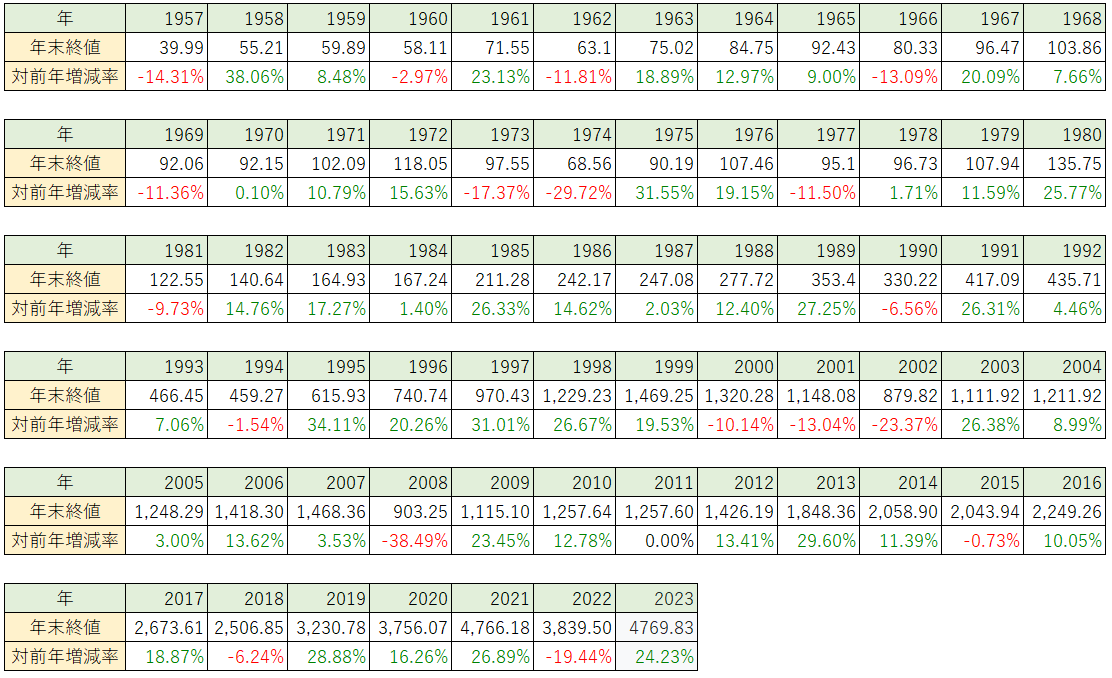
※S&P500データをもとに筆者が独自集計
時系列で見ると、所々対前年率割れが見られます。
おもな年度と前年増減率、出来事として、次の通りとなっています。
・2002年に同-23.37%(ITバブル崩壊)
・2008年に₋38.49%(リーマンショック/算出の中で最大の下げ幅)
・最近では2022年に₋19.44%(大幅利上げの実施)
オイルショックを除くと、2000年以降が比較的ボラティリティが大きな相場になっていました。
しかしながら、それらも乗り越えて、入れ替えはあるもののS&P500の銘柄は成長を続けていると言えるでしょう。
過去の平均成長率は?
データの中から過去どれぐらい指数が成長したかの年間平均成長率が算出できます。
具体的には以下の通りです。
・過去30年、1994年~2023年までの同数値は9.66%
・過去20年は9.00%、10年は11.02%、最近5年は15.36%
配当や税金を考えないリターンと見ても、時系列で一定水準を保って成長している(≒株価が上がっている)と見ることもできます。
おなじみのこちらの書籍には、S&P500のことや、インデックス投資の重要性についても紹介されています。
複利のロジックは?
代表的なアメリカの株価指数を確認したところで、本題の複利について確認しておきます。
単利と複利とは?
FP資格試験取得のために学習された方や、普段投資に接していらっしゃる方はおなじみの言葉ですが、改めて紹介します。
単利
例えば、何らかの投資対象に100万円を投資する場合、毎年利子(配当や利回りも含む)がつきます。
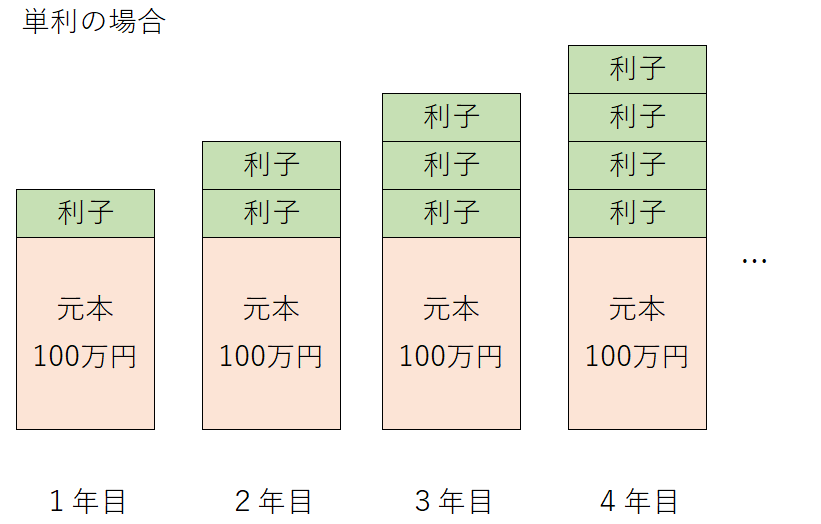
単利の場合は、その年の利子に対して再投資をせずに、生活費に回すなど元本100万円のみで運用すると考える場合です。
毎年100万円から受け取ることができる一定の利子はあるものの、単利の考え方には元本が増加することはありません。
100万円を例とした計算式は、
・毎年100万円×利率の分が利子として入る
・毎年利率に応じた利子を生む
という考え方です。
4年間で年の利率が5%の場合は
・元本+利子の総額は100万円+5万円×4年間=120万円
となります。
また、再投資をしない場合としては、
・受取利子・配当を他の利回りが良い金融商品や銘柄で運用している
などが考えられそうです。
複利
次に、今回のメインテーマとなる複利について紹介します。
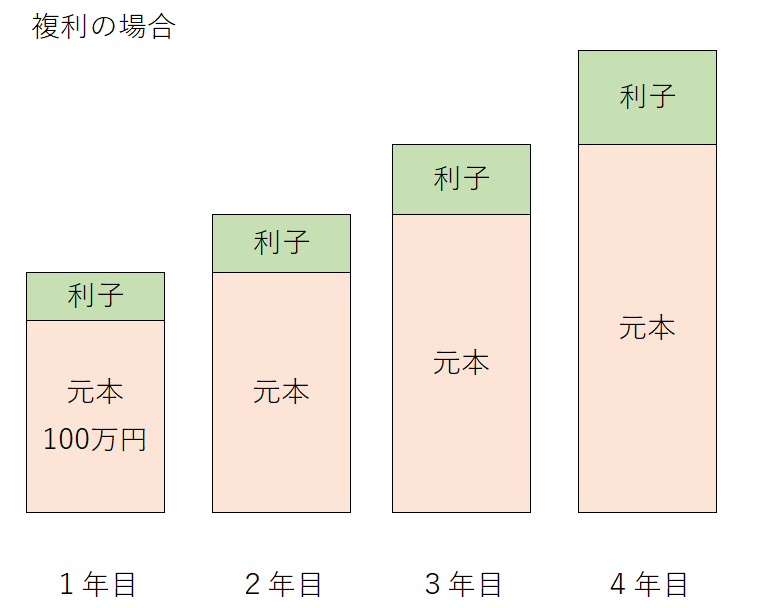
もともとの元本から生まれた利子についても、元本に加えて翌年の投資に回し、さらに翌々年も同様に実施する手法です。
元本がどんどん膨れ上がり、そこから生まれる利子も増えていくという考え方です。
100万円を例とした計算式としては、
ということになります。
n=4年の場合は^4(4乗)となり、(1+年間利率)を4回掛けるということになります。
すなわち、4年間で年利率が5%の場合は
という数式が成り立つこととなります。
シミュレーション結果のとおり、4年の成果として、
・複利が121.55万円
とその差1.55万円です。
しかしながら、後述しますが、複利の効果によってはその差がどんどん広がっていきます。
100万円を運用した場合の金額を確認
具体的に100万円を運用した場合の金額を、単利と複利で確認してみましょう。
年利を、タンス貯金の0%、余りつかない1%、少しつく5%、S&P500の66年間の平均増減率8.5%、そしてS&P500の過去30年の数値に近い10%で想定してみます。
単利
まず、単利の場合についてです。
ビジュアル的にグラフと、具体的な数字について紹介します。
グラフ推移
元金100万円が将来どのようになるのかの推移を、各利率で計算してみました。
以下、100万円を各利率で50年間寝かせた時の増え具合です。
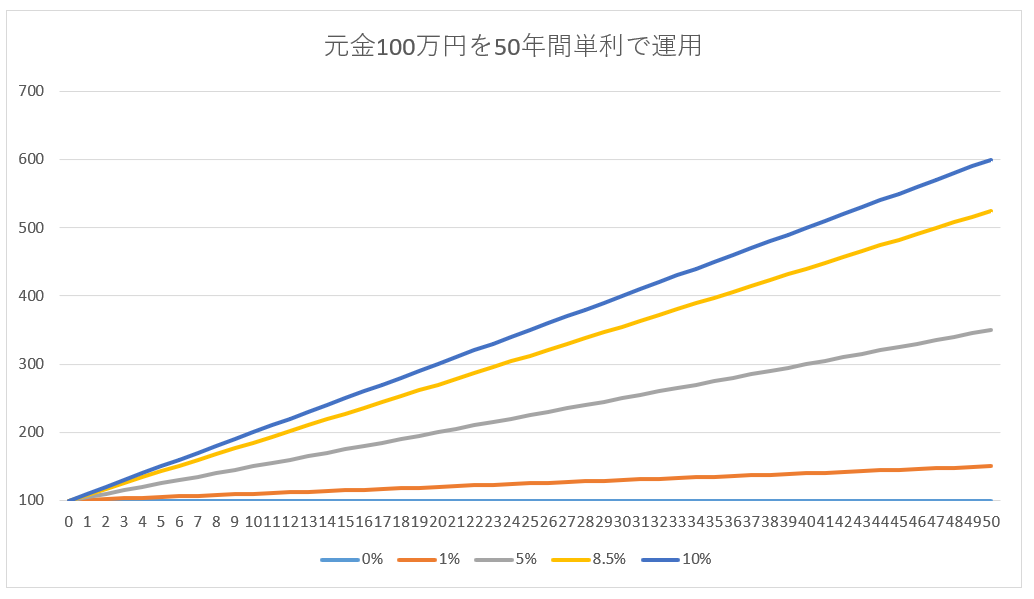
※筆者が独自作成
指数関数的に増えるのではなく、一次関数的に増えていくことがわかります。
次に、毎年100万円を追加して、単利で運用した場合のグラフです。

※筆者が独自作成
利率が高くなるにしたがって、20年目ぐらいから指数関数的に伸びているのが分かります。
数値推移
グラフのベースとなる、具体的な数値の推移です。
まず、100万円を各利率で50年間寝かせた時の数値です。

※筆者が独自作成
100万円をそのままにしているので、10%の運用を50年行っても、
にしかなりません。
対して、毎年100万円追加しながら単利で回した場合です。

※筆者が独自作成
この場合は、
・10%なら毎月の追加分も増えていくため、1億7,850万円まで増える
ということになります。
長期投資であれば、利息の恩恵に預かれるという感じでしょうか。
複利
続いて、同様の考え方で複利も見ていきましょう。
グラフ推移
まず、グラフ推移からです。
元本100万円をそのまま複利で運用した場合です。
100万円の株を買って配当は50年間に渡って同じ株に再投資するみたいなイメージでしょうか。
現実的にいえばS&P500指数のインデックス投資を行って置いておくイメージともいえるでしょう。
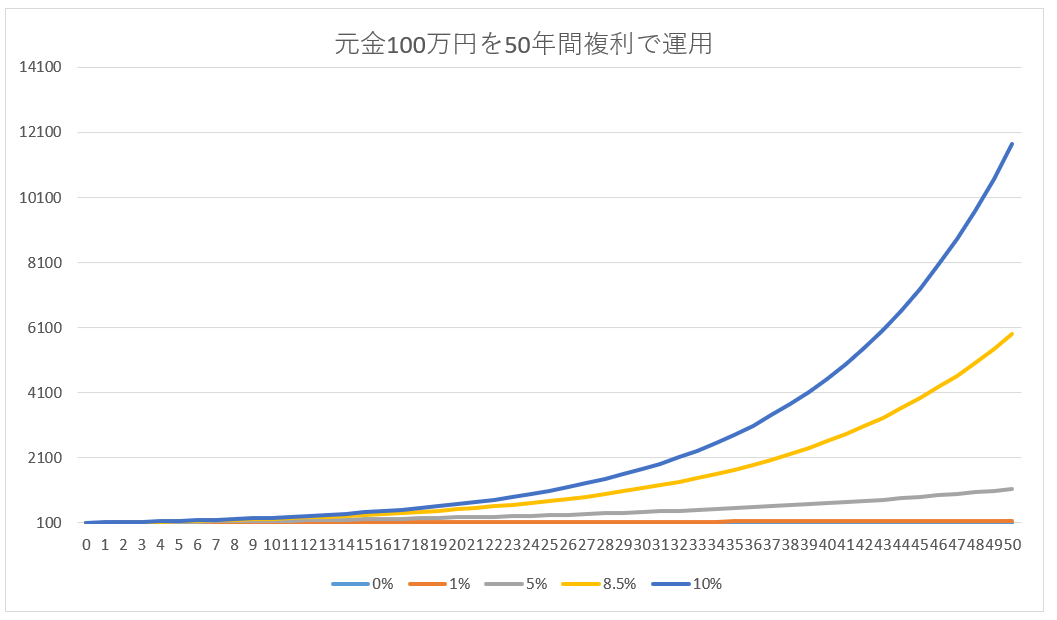
※筆者が独自作成
単利と比べて指数関数的に増加していることが分かります。
次に、毎年100万円を追加投資しながら、複利運用する場合はどうでしょうか?
イメージとしては、ドルコスト平均法でインデックス投資を行う感じです。

※筆者が独自作成
グラフは似ていますが、縦軸が1桁違っています。
こちらも10%はすごい勢いで伸びています。
ちなみに、S&P500の過去30年間の前年度比は平均ほぼ10%水準です。
したがって、これでも非現実的な数値ではないともいえます。
数値推移
最後に、これらの関数を構成する数値を確認します。

※筆者が独自作成
50年という期間で作成していますが、仮に
・30年間10%程度で運用できれば1,745万円にもなる
・50年間なら1億1739万円まで膨らむ
結果となります。
また、毎年100万円を追加しながら運用した場合の数値です。

※筆者が独自作成
同様に、
・10%運用なら+753万円の1,853万円
・さらに30年間頑張ると、元本3,100万円に対して8.5%運用なら+1億477万円の1億3,577万円、10%なら+1億5,094万円の1億8,194万円になる
・1億円を超えるのは10%運用なら25年目(元本2,600万円)、8.5%なら27年目(同2,800万円)、5%なら36年目(同3,700万円)
という効果が出ます。
そして、30年以降は、グラフと表からもわかる通り、複利の効果がどんどん発揮され、
指数的な数値として50年10%運用で総投資元本5,100万円に対して12億8,130万円という計算
ができます。
複利は時間を味方につける
複利で増えれば、利益確定して現預金を確保したいという気持ちになります。
しかしながら、当面使わない余剰資金はできれば複利の効果の恩恵に預かるべく、長期運用に回したい所でしょう。
iDeCoなどの長期に引き出せない資金は、この恩恵を多分に享受することも可能です。
将来のイメージは付きづらいですが、若い時からから少しずつ積立てることも要検討です。
結果的に、将来の年金不安もなくなることが期待できます。




コメント